|
|
|
|
|
|
|
|
Bei bekannter Ableitungsfunktion lassen sich die Nullstellen
einer Funktion 
iterativ nach Newton bestimmen:
Geometrische Deutung: die (
)-te verbesserte Näherung an die
Nullstelle ist die Nullstelle der Tangente des i-ten Wertes.
1) Gib Schätzwert 
der Nullstelle vor.
2) Setze 
= 
.
3) Berechne 
nach Vorschrift und setze 
.
4) Wiederhole Verfahren, bis der Fehler genügend klein ist.
5) Abbruchbedingung: 
,
n Anzahl der gewünschten exakten Stellen hinter dem Komma.
Bei sehr langsamer Konvergenz kann die Abbruchbedingung
erfüllt sein, obwohl die Nullstelle noch nicht erreicht ist.
Man schaue sich immer den Graph der Funktion an.
Hinreichende Bedingung für die Konvergenz des Newton-Verfahrens:
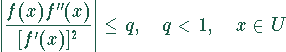
für alle x in einer Umgebung U der Nullstelle, die alle Punkte 
enthält.
In manchen Fällen konvergiert das Verfahren nicht oder sehr
langsam. Dann ist der Startwert 
zu weit von der Nullstelle entfernt
oder es handelt sich um eine mehrfache Nullstelle von f.
Ist die Nullstelle 
von f einfach, d.h., gilt 
und
, dann ist das Newton-Verfahren lokal quadratisch
konvergent (siehe dazu Konvergenzordnung),
Im Falle mehrfach zu zählender Nullstellen ist das Newton-Verfahren nur noch lokal linear konvergent,
Das Verfahren kann auch oszillieren oder in
Bereiche außerhalb des Definitionsbereiches der untersuchten
Funktion springen (z.B. 
).
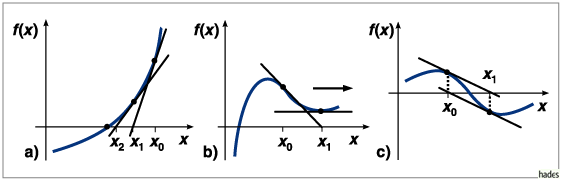
a) Newton-Verfahren, Gegenbeispiele: b) Verfahren divergiert, c) Verfahren oszilliert
|
|
|
|
|
|
|
|
