|
|
|
|
|
|
|
|
einer (oder mehrerer) Veränderlicher x.
Signalvektor, Darstellung eines Signals als ein Vektor 
,
, mit n Komponenten. Ein Signalvektor entsteht aus einer Signalfunktion durch
Diskretisierung:
an festgelegten Punkten 
.
Lineare Signalanalyse , Zerlegung eines Signalvektors 
,
, in eine Linearkombination bestimmter vorgegebener
Basisvektoren (Transformationsmatrix 
, 
), mit den
Koeffizienten 
( lineare Superposition):
Die verschiedenen Basisvektoren stehen für verschiedene
Eigenschaften des Signals. Die Koeffizienten 
beschreiben das
Signal; ihre Ermittlung ist die Aufgabe der Signalanalyse.
Fourieranalyse, wobei die Basisfunktionen Sinus- und Cosinusfunktionen zu
bestimmten Frequenzen 
sind. Die Fourierkoeffizienten 
zeigen die Anwesenheit einer Schwingung der Frequenz 
an.
Duale Basis, Satz von Vektoren 
, 
,
die so beschaffen sind, daß die Skalarprodukte des Signalvektors 
mit
den Vektoren 
die Koeffizienten des Signals ergeben, d.h. gerade die Signalanalyse durchgeführt wird.
Selbstduale Basis, eine Basis, in der die Basisvektoren und die
dualen Basisvektoren identisch sind.
Fourieranalyse und -synthese erfolgen beide durch Sinus- und
Cosinunsfunktionen; beide Basen sind also identisch.
Rechteckfunktionen als Basis: Eine Rechteckfunktion 
der Breite d
am Ort t ist eine Funktion, die zwischen 
und 
den Wert Eins,
außerhalb den Wert Null hat. Wählt man diese Funktionen als Basis, so zeigen
die Koeffizienten 
an, daß das Signal um den Zeitpunkt t
für die Dauer d vorlag.
Diese Basis ist übervollständig, denn jede Rechteckfunktion kann
z.B. durch ihre beiden Hälften, die wieder Rechteckfunktionen sind,
dargestellt werden.
Lineare Unabhängigkeit der Basis, die Eigenschaft, daß kein
Basisvektor als eine Linearkombination der anderen Basisvektoren
dargestellt werden kann.
Ist die Basis linear unabhängig, so sind die Koeffizienten eines Signals
eindeutig bestimmt.
Orthonormale Basis, eine Menge von Basisvektoren 
, in der
jeder Vektor normiert ist und orthogonal zu jedem anderen Vektor steht, d.h.
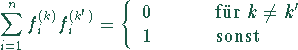
Eine orthonormale Basis ist linear unabhängig und selbstdual. Das
Skalarprodukt zweier Vektoren ändert sich nicht bei einer orthonormalen
Basistransformation.
Übervollständige Basis,
einem Signal können mehrere verschiedene
Koeffizientenvektoren zugeordnet werden.
Fourieranalyse, Charakterisierung eines Signals 
durch
die in ihm auftretenden (Kreis-)Frequenzen 
.
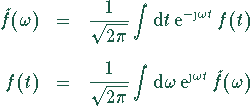
Die Fourierbasis ist selbstdual.
|
|
|
|
|
|
|
|
