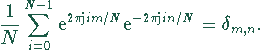Definition und Koeffizienten
Diskrete Fourier-Transformation,
diskrete Version der
kontinuierlichen Fourier-Transformation. Diese wird benutzt für Funktionen,
deren Werte in dem Intervall 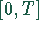 nur an diskreten Punkten
gegeben sind oder abgetastet werden.
nur an diskreten Punkten
gegeben sind oder abgetastet werden.
Entwicklung der Funktion in eine trigonometrische Summe:
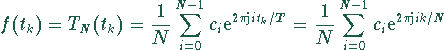
mit 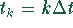 und
und 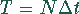 , wobei
, wobei  die
Gitterunterteilung ist. In der Meßtechnik wird
die
Gitterunterteilung ist. In der Meßtechnik wird  auch als
Abtastperiode bezeichnet und entsprechend ist die Abtastfrequenz
auch als
Abtastperiode bezeichnet und entsprechend ist die Abtastfrequenz
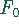 das Inverse der Abtastperiode:
das Inverse der Abtastperiode: 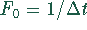 .
.
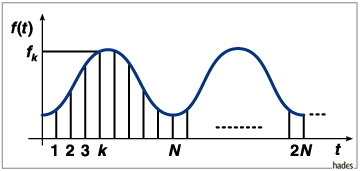
Schematische Darstellung einer diskreten periodischen Funktion
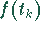
Koeffizient der diskreten Fourier-Transformation, vgl. mit
Koeffizienten der Fourier-Reihe und des
Fourier-Integrals:
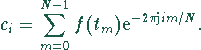
Notation: Für 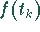 wird oft auch einfach
wird oft auch einfach 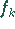 geschrieben.
geschrieben.

- Der Vorfaktor
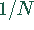 kann wie der Faktor
kann wie der Faktor 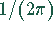 beim
Fourier-Integral auf drei
Arten aufgeteilt werden (vgl. Anmerkung bei komplexer Darstellung des
Fourier-Integrals). Hier soll der Vorfaktor vor der Summe von
beim
Fourier-Integral auf drei
Arten aufgeteilt werden (vgl. Anmerkung bei komplexer Darstellung des
Fourier-Integrals). Hier soll der Vorfaktor vor der Summe von 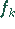 stehen.
stehen.
- Die Koeffizienten
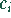 folgen aus der Orthogonalität der
Funktionen
folgen aus der Orthogonalität der
Funktionen  (
(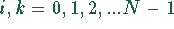 ):
):
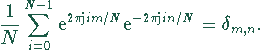
- Die diskrete Fourier-Transformation kann auch als
trigonometrische Interpolation der Funktion
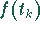 aufgefaßt
werden, weil an den Gitterpunkten gilt:
aufgefaßt
werden, weil an den Gitterpunkten gilt: 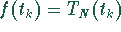 und für
beliebige Punkte t aus
und für
beliebige Punkte t aus 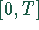 :
: 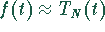 .
.
- Der Vektor
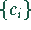 heißt auch diskrete Fourier-Transformierte
von
heißt auch diskrete Fourier-Transformierte
von 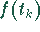 und der Übergang
und der Übergang 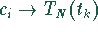 diskrete inverse
Fourier-Transformation.
diskrete inverse
Fourier-Transformation.
- Bei der diskreten Fourier-Transformation gelten dieselben
Symmetrien wie
bei der kontinuierlichen Fourier-Transformation.













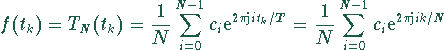
![]() und
und ![]() , wobei
, wobei ![]() die
Gitterunterteilung ist. In der Meßtechnik wird
die
Gitterunterteilung ist. In der Meßtechnik wird ![]() auch als
Abtastperiode bezeichnet und entsprechend ist die Abtastfrequenz
auch als
Abtastperiode bezeichnet und entsprechend ist die Abtastfrequenz
![]() das Inverse der Abtastperiode:
das Inverse der Abtastperiode: ![]() .
.
![]()
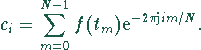
![]() wird oft auch einfach
wird oft auch einfach ![]() geschrieben.
geschrieben.