|
|
|
|
|
|
|
|
) werden ausschließlich nach dem Sinus entwickelt:
mit den Koeffizienten
Sowohl bei der Fourier-Reihe für gerade Funktionen als auch bei
der für ungerade ist der Integrand der zu den entsprechenden
Fourier-Koeffizienten gehörigen Integrale eine gerade Funktion.
Deshalb braucht man nicht über das ganze Intervall 
zu
integrieren, sondern nur über das halbe Intervall 
:
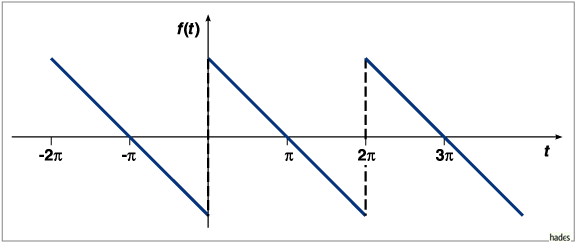
Sägezahnfunktion mit negativer Steigung
Entwicklung der ungeraden Sägezahn-Funktion
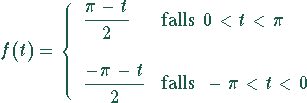
mit der Periodendauer 
in eine Fourier-Reihe.
Für die Koeffizienten
erhält man (
) mit Hilfe der Produktintegration:
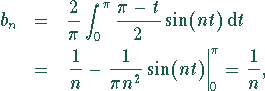
wobei 
ist und 
, 
ergibt. Also lautet die
Fourier-Reihe dieser Funktion:
|
|
|
|
|
|
|
|
