|
|
|
|
|
|
|
|
Determinanten höherer Ordnung lassen sich durch Determinanten
niedriger Ordnung, sogenannte Unterdeterminaten,
berechnen.
Berechnung von Determinanten dritter Ordnung
kann man zurückführen auf die Berechnungen von Determinanten zweiter Ordnung.
Analog für Determinanten mit höherer Ordnung.
Unterdeterminante zweiter Ordnung, 
,
entsteht aus einer
Determinante durch Streichen der i-ten Zeile und der k-ten
Spalte: Die verbleibenden Elemente bilden eine zweireihige
Determinante.
Adjungierte Unterdeterminante
des Elementes 
, die Unterdeterminante 
multipliziert mit dem Vorzeichenfaktor 
Dreireihige Determinanten sind durch Ausklammern der
Elemente der ersten Zeile mit Unterdeterminanten zweiter Ordnung
darstellbar.
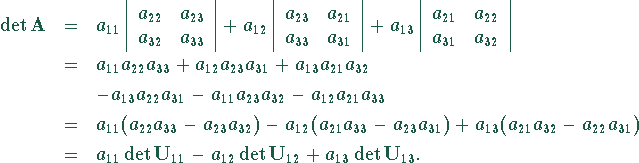
Oder
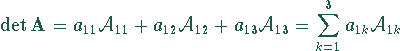
Elemente der ersten Zeile der Matrix 
werden
ausgeklammert, die Determinante ist ein Ausdruck, in dem diese
Elemente der ersten Zeile und ihre Adjunkten auftreten, daher:
Entwicklung der Determinante nach den Elementen der ersten Zeile.
Entsprechende Entwicklungsformeln gibt es für jede andere Zeile oder Spalte:
|
|
|
|
|
|
|
|
