|
|
|
|
|
|
|
|
Die Polytropengleichung liefert für den Druck die Beziehung
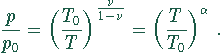
Dabei ist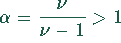 
.
Berechnen Sie unter Benutzung des Mittelwertsatzes der Differentialrechnung
die untere und obere Schranke für die
Druckdifferenzen beim Anstieg der Temperatur von 
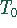auf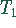 
.
Lösung:
Da der funktionale Zusammenhang zwischen Druck und Temperatur in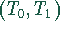 
differenzierbar
und stetig ist, kann der Mittelwertsatz der Differentialrechnung angewendet werden.
Nach diesem Satz gilt
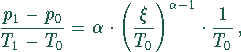
dabei ist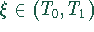 
.
Daraus folgt für die Druckdifferenz
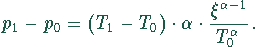
Die untere Schranke wird bei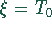 
erreicht, d.h.
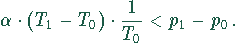
An der oberen Schranke ist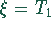 
, d.h.,
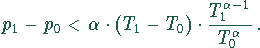
Damit ergibt sich für die Abschätzung
